Economics at Zero Marginal Cost: Chain Rule

Chain Rule

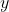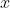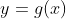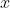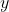If we have a differentiable function $z=f(y),$ where $y$ is in turn a differentiable function of another variable $x$ , say $y=g(x)$ , then the derivative of $z$ with respect to $x$ is equal to the derivative of $z$ with respect to $y$ , times the derivative of 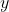$y$ with respect to $x$ .

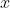Symbolically,

$\frac{dz}{dx} = \frac{dz}{dy}\frac{dy}{dx}=f'(y)g'(x)$

This rule is known as chain rule.

In view of the function 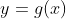$y=g(x)$ , we can expressed the function $z=f(y)$ as $z=f[g(x)]$ .

$f[g(x)]$ is the composite function that is formed when $g(x)$ is substituted for $y$ in $f(y)$ .

$f[g(x)]$ is read as " $f$ of $g$ of $x$ ".

A composite function is a function that depends on another function. A composite function is created when one function is substituted into another function.

It is for this reason that the chain rule is also referred to as composite function rule or function of a function rule.

Excercise:

1. Given $y=u^3 +2u,$ where $u=5-x^2,$ find $dy/dx$ by the chain rule.

Solution:

Given: $y=u^3 +2u,$ and $u=5-x^2,$

To find: $dy/dx$

$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$

$\\\frac{dy}{du}=\frac{d}{du}y=\frac{d}{du}(u^3+2u)\\ \frac{dy}{du}=(\frac{d}{du}u^3+\frac{d}{du}2u)\\ \frac{dy}{du}=3u^{3-1}+2\frac{d}{du}u\\ \frac{dy}{du}=3u^2+2.1\\ \frac{dy}{du}=3u^2+2\\$

$\\\frac{du}{dx}=\frac{d}{dx}u=\frac{d}{dx}(5-x^2)\\ \frac{du}{dx}=\frac{d}{dx}5-\frac{d}{dx}x^2\\ \frac{du}{dx}=0-2x^{2-1}\\ \frac{du}{dx}=-2x\\$

$\\\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}\\ \frac{dy}{dx}=(3u^2+2).-2x\\ \frac{dy}{dx}=-2x(3u^2+2)\\$

Substituting $u=5-x^2$

$\\\frac{dy}{dx}=-2x(3(5-x^2)^2+2)\\ \frac{dy}{dx}=-2x(3(25-10x^2+x^4)+2)\\ \frac{dy}{dx}=-2x(75-30x^2+3x^4+2)\\ \frac{dy}{dx}=-150x+60x^3-6x^5-4x\\ \frac{dy}{dx}=-154x+60x^3-6x^5$

2. Given $w=ay^2$ , and $y=bx^2+cx$ find $dw/dx$ by the chain rule

Solution:

Given: $w=ay^2$ and $y=bx^2+cx$

To find: $dw/dx$

$\\\frac{dw}{dx}=\frac{dw}{dy}\frac{dy}{dx}\\ \frac{dw}{dy}=\frac{d}{dy}w=\frac{d}{dy}(ay^2)\\ \frac{dw}{dy}=a\frac{d}{dy}y^2\\ \frac{dw}{dy}=a.2y^{2-1}\\ \frac{dw}{dy}=2ay$

$\\\frac{dy}{dx}=\frac{d}{dy}y=\frac{d}{dx}(bx^2+cx)\\ \frac{dy}{dx}=\frac{d}{dx}bx^2+\frac{d}{dx}cx\\ \frac{dy}{dx}=b\frac{d}{dx}x^2+c\frac{d}{dx}x\\ \frac{dy}{dx}=b.2x^{2-1}+c.1\\ \frac{dy}{dx}=2bx+c$

$\\\frac{dw}{dx}=\frac{dw}{dy}\frac{dy}{dx}\\ \frac{dw}{dx}=2ay(2bx+c)$

Substituting $y=bx^2+cx$

$\\\frac{dw}{dx}=2a(bx^2+cx)(2bx+c)\\ \frac{dw}{dx}=2a(2b^2x^3+bcx^2+2bcx^2+c^2x)\\ \frac{dw}{dx}=2ax(2b^2x^2+bcx+2bcx+c^2)\\ \frac{dw}{dx}=2ax(2ab^2x^2+abcx+2abcx+2ac^2)$

Economics at Zero Marginal Cost

Pages

Wednesday, June 10, 2020

Chain Rule

No comments:

Post a Comment

Disturbance term/Error term

Contact Form