If 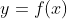 then
then  is the first derivative of the function.
is the first derivative of the function.
Since the first derivative 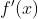 is
itself a function (i.e., a derived function from a primitive
function
is
itself a function (i.e., a derived function from a primitive
function 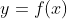 , it too should be differentiable with respect
to , provided it is
continuous and smooth.
, it too should be differentiable with respect
to , provided it is
continuous and smooth.
The first derivative can, therefore, be differentiated again and the result of this differentiation known as the second derivative of the function is denoted by:
Again, since the second
derivative is a function of , it can be differentiated with respect to
again to produced a third
derivative, which in turn can be the source of a fourth derivative, and so on
as long as differentiability condition is met.
Given a function
First Derivative:
Derivatives of higher order can be represented as:
Second Derivative:
Third Derivative: 
Fourth Derivative: 
Exercise:
Find the second and third derivatives of the
following:
1.
Solution:
First derivatives:
Second derivative:
Third derivative:
2. 
Solution:
First derivative:
Second derivative:
Third derivative:


No comments:
Post a Comment