Explicit and Implicit Function
A function given in the form of , say,
is called an explicit
function, because the variable
is
explicitly expressed as a function of
.
A function in which the dependent variable is
not isolated on one side of the equation is known as an implicit function. For example, the equation represents an implicit function. Implicit
functions are usually given in terms of both
dependent and independent variables.
Exercise:
Find 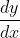
1. 
Solution:
Given:
Differentiating
both sides with respect to .
2.
Solution:
Given:
Differentiating both sides with respect to .
3.
Solution:
Given:
Differentiating both sides with respect to 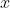 .
.
4.
Solution:
Given:
Differentiating both sides with respect to 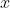 .
.


No comments:
Post a Comment