Economics at Zero Marginal Cost: Functions and Its Types

A function is a mathematical relationship between the dependent variable and independent variable(s). If y changes with respect to change in x, then y is said to be a function of x and the relationship is denoted by 𝒚 = 𝒇(𝒙) which is read as: " y equals f of x ".

In the function, y is the dependent variable and x is the independent variable. The dependent variable as the name suggest cannot change by itself and its value may vary with the change in the independent variable(s). An independent variable may take any value. Alternatively, x is also referred to as an argument of the function and y is referred to as the value of the function.

The set of all permissible values that x can take in a given context is known as the domain of the function, which may be a subset of the set of all real numbers. The set of all values that y can take is known as the range of the function.

Example:

Let us understand the concept of a function with the help of an example:

𝒚=𝒇(𝒙)=𝟐𝒙

Let us assume that x takes the value of greater than or equal to 1 and less than or equal to 3.

Domain of the function: 1 ≤ 𝑥 ≤ 3

When x = 1

y= 2x = 2(1) = 2

When x = 2

y= 2x = 2(2) = 4

When x = 3

y= 2x = 2(3) = 6

∴ Range of the function: 2 ≤ 𝑥 ≤ 6

A function is also called mapping or transformation which implies the action of associating one thing with another. The y value into which the x value is mapped is called the image of that x value.

The functional notation f implies a rule by which the set x is "mapped" (transformed) into the set y.

Algebraic Functions:

A function consisting of a finite number of terms involving powers and roots of the variable 𝒙 and the four basic mathematical operations (addition, subtraction, multiplication and division) is called an algebraic function.

There are two categories of algebraic functions namely : explicit and implicit algebraic functions.

A function given in the form of 𝒚=𝒇(𝒙), say, $y=f(x)=3x^4$ is called an explicit function, because the variable 𝒚 is explicitly expressed as a function of 𝒙.

A function in which the dependent variable is not isolated on one side of the equation is known as an implicit function. For example, the equation $x^2+xy-y^2=1$ represents an implicit function. Implicit functions are usually given in terms of both dependent and independent variables.

Constant functions:

A function whose range consists of only one element is called a constant function.

Example:

𝒚 = 𝒇(𝒙) =𝟑

or, 𝒚 = 𝟑

or, 𝒇(𝒙) = 𝟑

The value of y remains the same regardless of the value of x. If we plot a constant function on a coordinate plane it will appear as a horizontal straight line. Let us plot the function, 𝒚 = 𝒇(𝒙)= 𝟑.

Polynomial function:

A polynomial function is a function involving only non-negative integer powers of x. The word polynomial means "multi-term" and a polynomial function of a single variable x has the general form:

$\\y=a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+...+a_{n}x^{n}\\ or, \\y=a_{0}.1+a_{1}x+a_{2}x^{2}+...+a_{n}x^{n}\\ or, \\y=a_{0}+a_{1}x+a_{2}x^{2}+...+a_{n}x^{n}\\$

Each term has a co-efficient and a non-negative integer power of the variable x.

Depending on the highest power of 𝒙 (i.e., the value of the integer of 𝒙), there are several sub-classes of polynomial function.

If the highest power of a polynomial function is zero that is n=0, then we have a constant function. Hence, a constant function is a subclass of polynomial function.

If $\\y=a_{0}x^{0}=a_{0}.1\\$

or, $\\y=a_{0}$

then the function is a constant function.

Linear Functions:

If the highest power of a polynomial function is one that is, n=1 then we have a linear function.

If $y=a_{0}x^{0}+a_{1}x^{1}\\$

or, $y=a_{0}+a_{1}x\\$

then the function is a linear function.

If we plot a linear function on a coordinate plane it will appear as a straight line.

Let us graph the following linear functions:

1. 𝒚 = 𝟐𝒙+𝟕
2. 𝒚 = 𝟓𝒙−𝟑
3. 𝒚 = −𝟒𝒙+𝟓
4. 𝒚 = −𝟐𝒙

1. 𝒚 = 𝟐𝒙+𝟕

The function is in the form of $\\y=a_{0}+a_{1}x$

$a_{0}\rightarrow y-intercept$ and $a_{1}\rightarrow slope$

$a_{0}= 7\\$ $a_{1}= 2\\$

2. 𝒚 = 𝟓𝒙−𝟑

The function is in the form of $\\y=a_{0}+a_{1}x$

$a_{0}\rightarrow y-intercept$ and $a_{1}\rightarrow$ slope

$a_{0}= -3\\$ $a_{1}= 5\\$

3. 𝒚 = −𝟒𝒙+𝟓

The function is in the form of $\\y=a_{0}+a_{1}x$

$a_{0}\rightarrow y-intercept$ and $a_{1}\rightarrow slope$

$a_{0}= 5\\$ $a_{1}= -4\\$

4. 𝒚 = −𝟐𝒙

The function is in the form of $\\y=a_{0}+a_{1}x$

$a_{0}\rightarrow y-intercept$ and $a_{1}\rightarrow slope$

$a_{0}= 0\\$ $a_{1}= -2\\$

Quadratic Functions:

If the highest power of a polynomial function is two that is, n=2 then we have a quadratic function.

If $\\y=a_{0}+a_{1}x+a_{2}x^{2}\\$ then the function is a quadratic function.

If we plot a quadratic function on a coordinate plane it will appear as a parabola that is a curve with a single built-in bump or wiggle. It has only one turning point.

If $a_{2}>0$ , the shape of the curve will be a valley.

If $a_{2}<0$ , the shape of the curve will be a hill.

Let us graph the following functions:

$\\1. y=3x^{2}+2x+5\\ 2. y=-4x^{2}+5x-4\\ 3. y=5x^{2}+2x\\ 4. y=-3x^{2}\\$

$\\1.\ y=3x^{2}+2x+5\\$

The function is in the form of $\\y=a_{0}+a_{1}x+a_{2}x^{2}$

$a_{0}\rightarrow y-intercept$

$a_{0}=5$ $a_{2}=3>0$

$2.\ y=-4x^{2}+5x-4\\$

The function is in the form of $\\y=a_{0}+a_{1}x+a_{2}x^{2}$

$a_{0}\rightarrow y-intercept$

$a_{0}=-4$ $a_{2}=-4<0$

$3.\ y=5x^{2}+2x\\$

The function is in the form of $\\y=a_{0}+a_{1}x+a_{2}x^{2}$

$a_{0}\rightarrow y-intercept$

$a_{0}=0$ $a_{2}=5>0$

$4.\ y=-3x^{2}\\$

The function is in the form of $\\y=a_{0}+a_{1}x+a_{2}x^{2}$

$a_{0}\rightarrow y-intercept$

$a_{0}=0$ $a_{2}=-3<0$

Cubic Functions:

If the highest power of a polynomial function is three that is, n=3 then we have a cubic function.

If $\\y=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}$ then the function is a cubic function.

If we plot a cubic function on a coordinate plane it will have two wiggles. A cubic could have up to two turning points.

Types of Polynomial Functions:

Rational functions:

A rational function is any function which can be written as the ratio of two polynomial functions, where the polynomial in the denominator is not equal to zero. The general form is written as:

$f(x)=\frac{P(x)}{Q(x)}$

The domain of function is the set of all values of x for which the denominator 𝑸(𝒙 ) is not zero.

Example: $y=\frac{2x+1}{x^{2}+5x+3}$ is a rational function.

A special rational function that has interesting application in economics is the function $y=\frac{a}{x}$ or $xy=a$ which plots a rectangular hyperbola.The product of the two variables 𝒙 and 𝒚 is always a fixed constant 𝒂.

The function may be used to represent a special demand curve for which the total expenditure 𝑷𝑸 is constant all levels of price. It may also be use to represent the average fixed cost (AFC) curve. The AFC curve must be rectangular hyperbola because AFC x Q (= TFC ) is a fixed constant.

The rectangular hyperbola obtain by plotting the function 𝒚=𝒂/𝒙 or 𝒙𝒚=𝒂 on a coordinate plane never touches either of the axes, even if the curve is extended upward and to the right.

As the value of x and y becomes very large, the curve will get closer and closer to the x-axis and y-axis but never actually touches it.

Non-algebraic Functions (Transcendental Functions):

All functions which are not algebraic are called transcendental functions. These functions include:

1. Exponential Functions

2. Logarithmic Functions

3. Trigonometric Functions

Exponential Functions:

A function having a constant base and a variable exponent is called an exponential function. In other words, an exponential function is a function whose independent variable appears in the role of an exponent. For example, $y=b^{x}$ exponential functions in which the base 𝒃 is a constant and the exponent 𝒙 is a variable.

$y=b^{x}$

For $b>0$

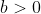
In economics, exponential functions are useful for describing sharp increase and decrease in the value of dependent variable.

Logarithmic Functions:

When a variable is expressed as a function of the logarithm of another variable, the function is referred to as logarithmic function. A logarithmic function is expressed as:

$y=Log_{a}x$

where 𝒂 > 𝟎 , 𝒂 ≠ 𝟏 is the base. It is read as“y is the log to the base a of x”.

If we expressed the logarithmic function $y=Log_{a}x$ by the equation

$x=a^{y}$

then it is an exponential function.

Thus, logarithmic and exponential functions are inverse functions, i.e., if 𝒙 is an exponential function of 𝒚, then 𝒚 is the logarithmic function of 𝒙.

Although the base of logarithm can be any positive number other than 1, but most widely used bases are either 𝟏𝟎 (common logarithms) or 𝒆 = 𝟐.𝟕𝟏𝟖 (natural logarithms)

By convention, 𝐥𝐨𝐠⁡ 𝒙 denotes the common logarithm of 𝒙 and 𝐥𝐧 ⁡𝒙 denotes natural logarithm of 𝒙.

If any other base is meant, it is specified.

$y=Log_{a}x$

For $a>1$

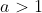
Trigonometric Functions:

Trigonometric functions also called circular functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. The most widely used trigonometric functions are the sine, the cosine, and the tangent.

The trigonometric functions are very useful in the study of business cycles, seasonal or other cyclic variations are described by sine or cosine functions.

Sine Function: