Simultaneous Equations of n variables and n equations:
Re-writing the above set of simultaneous equations in matrix form, we have
Let,
Cramer's Rule:
Steps:
First find the determinant of A, i.e.,|A|
Next, find the determinant of 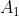 i.e.,
i.e.,  and then divide it by |A| to obtain the value of
and then divide it by |A| to obtain the value of 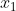 .
.
i.e.,
Next, find the determinant of 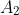 i.e.,
i.e.,  and then divide it by |A| to obtain the value of
and then divide it by |A| to obtain the value of 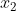 .
.
i.e.,
Next, find the determinant of  i.e.,
i.e.,  and then divide it by |A| to obtain the value of
and then divide it by |A| to obtain the value of 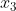 .
.
i.e.,
Next, find the determinant of 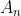 i.e.,
i.e.,  and then divide it by |A| to obtain the value of
and then divide it by |A| to obtain the value of 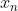 .
.
i.e.,
1. Solve the following equations by Cramer’s rule:
Solution:
Given: System of simultaneous equations
To find: The values of 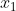 and
and 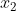 .
.
Re-writing the equations in matrix form:
Let
Now,
Next,


No comments:
Post a Comment