Static (Equilibrium) Analysis
What is a Static Analysis?
An equilibrium is defined as a constellation of selected interrelated variables so adjusted to one another that no inherent tendency to change prevails in the model which they constitute. An equilibrium for a specified model is a situation characterised by a lack of tendency to change. It is for this reason that the analysis of equilibrium or the study of what the equilibrium state is like is referred to as statics.
In static economic analysis, time element has nothing to do. All economic variables refer to the same point of time. A static analysis does not show the path of change. It only tells about the condition of equilibrium.
Francois Quesnay had developed a cruder version of this technique called Tableau économique, and Léon Walras's work Elements of Pure Economics on general equilibrium theory also was a forerunner and made a generalization of Leontief's seminal concept. In its modern form, the I-0 analysis has been developed by the American economist Wassily W. Leontief in his famous work 'Structure of the American Economy' in the year 1951.
Wassily Leontief (August 5, 1905 – February 5, 1999), was a Russian- American economist known for his research on input-output analysis and how changes in one economic sector may affect other sectors. Leontief won the Nobel Committee's Nobel Memorial Prize in Economic Sciences in 1973, and four of his doctoral students have also been awarded the prize (Paul Samuelson 1970, Robert Solow 1987, Vernon L. Smith 2002, Thomas Schelling 2005).
At static level, the Input-output model deal with a particular question:
"What level of Output should each of the n - industry produce in order that, it will just be sufficient to satisfy the total demand for that product"
Introduction:
Input-Output analysis is a method of analysing how an industry undertakes production by using the output of other industries in the economy and how the output of the given industries used up in other industries or sectors. Since various industries are interdependent, i.e., the output of one industry is an input for the others, their mutual relationship ultimately must lead to equilibrium between supply and demand in the economy consisting of 'n' industries.
Input-Output Analysis is also known as the inter-industry analysis as it explains the interdependence and interrelationship among various industries. In other words, the Input-Output Analysis explains the interdependence of inputs and outputs of various industries in the economy.
The Open Model:
The commodity produced by n-industries will be used as intermediate inputs i.e., input supplied by the n-industries together with Primary Inputs (Raw materials, land, labour, etc.) which are not industrial products. If there are n-industries in an economy, then the products of these nindustries will be use as input demand of the same n-industries i.e., which is to be use for further production of any commodity of the n-industries. Some quantity of the commodity produced by n-industries will be use as final demand i.e., they will be consumed as final goods by consumers and not for further production.
A Closed Model is one in which the output of the n-industries in the economy is used entirely as inputs in the n-industries and hence totally absorbed in to the system. An Open Model is one in which the output of the n-industries is used as intermediate inputs in the production of commodity in the n-industries (INPUT DEMAND) as well as final goods consumed by consumers (FINAL DEMAND). As such the Open Model accommodate the activities of the n-industries as well as those of the consumer households, government sector and foreign sector.
Assumptions:
1. Each industry produces only one homogeneous commodity.
2. Each Industry uses a fixed input ratio or factor combination for the production of its output.
3. Production in every Industry is subject to CRS, so that a k-fold change in every input will result in exactly k-fold change in the output.
4. If an industry produces two different commodities or uses two different possible factor combinations, then that industry may be broken down in to two separate industries.
Input-Output Table:
Input-output table shows the disposition of the total products and total inputs among the different industries. Let us assume that an economy consists of 3 producing sectors only; and that the production of each sector is being used as the input in all the sectors and used for final consumption.
For an 3-industry Economy
In the table,  are total outputs of 3 sectors and
are total outputs of 3 sectors and  is the amount of output of the 𝒊𝒕𝒉 industry used up as an intermediary input by the 𝒋𝒕𝒉 industry ( i, j = 1,2,3). The 'total output' columns gives the overall input and output of each commodity. The first column describes the input or cost structure of the first industry:
is the amount of output of the 𝒊𝒕𝒉 industry used up as an intermediary input by the 𝒋𝒕𝒉 industry ( i, j = 1,2,3). The 'total output' columns gives the overall input and output of each commodity. The first column describes the input or cost structure of the first industry: 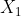 units of output of the first industry was produced with the use of
units of output of the first industry was produced with the use of  units of first good,
units of first good,  units of second good, and
units of second good, and  units of 3rd good, and
units of 3rd good, and 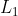 units of labor. Similar meanings will follow for other columns, i.e., output
units of labor. Similar meanings will follow for other columns, i.e., output 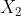 and
and 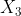 .
.
Technological Coefficient Matrix:
From the assumption of fixed input requirements, we see that in order to produce one unit of 𝒋𝒕𝒉 commodity, the input used of 𝒊𝒕𝒉 commodity must be a fixed amount, which we denote by 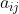 ; thus
; thus  . If
. If 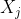 represents the total output of the 𝒋𝒕𝒉 commodity (or 𝒋𝒕𝒉 producing sector) the input requirements of the 𝒊𝒕𝒉 commodity will be equal to
represents the total output of the 𝒋𝒕𝒉 commodity (or 𝒋𝒕𝒉 producing sector) the input requirements of the 𝒊𝒕𝒉 commodity will be equal to  or
or  .
.
Now,
In general terms, demand for the product of each industry is written as:
or,
If Industry I produce an output just sufficient to meet the input requirements of the 3-industries as well as the final demand of the open sector, its output level  must satisfy the following equation:
must satisfy the following equation:
In the similar manner, the output levels of other 2 industry must satisfy the following equations:
Moving all terms involving variable 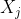 to the left hand side, we have
to the left hand side, we have
Simplifying ,
Simplifying further,
Re-writing in matrix form,
Let co-efficient matrix be A, Variable Vector be X and constant term Vector be F
Hence, AX = F
Re-arranging for co-efficient matrix A,
or, 
Multiplying both sides by 
or,  (
( )
)
Where, ( 𝑰 − 𝑨) → Leontief matrix, X → Variable vector and F → Constant term vector
As long as Leontief Matrix ( 𝑰 − 𝑨) is non-singular , we are able to find its inverse  and obtain the unique solution of the system.
and obtain the unique solution of the system.
The Generalised n-industries Case
Input-Output Table for n-industries Case
The input-output table shows the disposition of the total products and total inputs among the different industries. Let us assume that an economy consists of producing sectors only; and that the production of each sector is being used as the input in all the sectors and used for final consumption.
In the table,  are total outputs of n sectors and
are total outputs of n sectors and  is the amount of output of the ith industry used up as an intermediary input by the jth industry ( i, j = 1,2,..,n). The 'total output' columns gives the overall input and output of each commodity. The first column describes the input or cost structure of the first industry:
is the amount of output of the ith industry used up as an intermediary input by the jth industry ( i, j = 1,2,..,n). The 'total output' columns gives the overall input and output of each commodity. The first column describes the input or cost structure of the first industry: 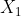 units of output of the first industry was produced with the use of
units of output of the first industry was produced with the use of  units of first good,
units of first good,  units of second good, and
units of second good, and  units of nth good, and
units of nth good, and 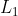 units of labor. Similar meanings will follow for other columns, i.e., output
units of labor. Similar meanings will follow for other columns, i.e., output 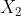 and
and 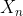 .
.
Now suppose that each unit of output of each industry has a price of ₹100 (say). Then each entry of the above table can be expressed in terms of money value (rather than being a physical unit). It is then possible to add down the columns. The sum of each column gives the total cost of the corresponding industry.
Technological Coefficient Matrix:
From the assumption of fixed input requirements, we see that in order to produce one unit of 𝒋𝒕𝒉 commodity, the input used of 𝒊𝒕𝒉 commodity must be a fixed amount, which we denote by 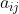 ; thus
; thus  . If
. If 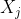 represents the total output of the 𝒋𝒕𝒉 commodity (or 𝒋𝒕𝒉 producing sector) the input requirements of the 𝒊𝒕𝒉 commodity will be equal to
represents the total output of the 𝒋𝒕𝒉 commodity (or 𝒋𝒕𝒉 producing sector) the input requirements of the 𝒊𝒕𝒉 commodity will be equal to  or
or  .
.
Now,
In general terms, demand for the product of each industry is written as:
or,
If Industry I produce an output just sufficient to meet the input requirements of the 3-industries as well as the final demand of the open sector, its output level  must satisfy the following equation:
must satisfy the following equation:
In the similar manner, the output levels of other n-industry must satisfy the following equations:
Moving all terms involving variable  to the left hand side, we have
to the left hand side, we have
Simplifying ,
Simplifying further,
Re-writing in matrix form,
Let co-efficient matrix be 𝐀, Variable Vector be X and constant term Vector be 𝐅
Hence, AX = F
Rearranging for co-efficient matrix A
or, 
Multiplying both sides by 
or,  (
( )
)
Where, ( 𝑰 − 𝑨) → Leontief matrix, X → Variable vector and F → Constant term vector
As long as Leontief Matrix ( 𝑰 − 𝑨) is non-singular , we are able to find its inverse  and obtain the unique solution of the system.
and obtain the unique solution of the system.




No comments:
Post a Comment