Isoquants

An isoquant is the locus of points representing different combinations of two inputs, say labour and capital yielding the same level of output. In other words, an isoquant includes efficient methods or all the combinations of factors of production for producing a given level of output. An isoquant is also called an equal-product curve.

Tabular and Graphical Representation:

The factor combinations are so formed that the substitution of one factor for the other leaves the output unaffected.

Factor Combinations	Labour (L)	Capital (K)	Output (Q)
A	1	12	100
B	2	8	100
C	3	5	100
D	4	3	100
E	5	2	100

The isoquant curve all along its length represents a fixed quantity, Q=100. For instance, points A, B, C, D, and E on the isoquant Q represent four combinations of inputs, L and K, as shown in Table 1, all yielding the same output of 100 units. The movement from A to E indicates decreasing capital (K) and increasing labour (L). If labour decreases and capital increases, output remains the same, vice versa.

Isoquant Map:

An isoquant map is a set of isoquants. Each isoquant shows various combinations of two inputs that can be used to produce a given level of output. An upper isoquant is formed by a greater quantity of one or both of the inputs than that indicated by the lower isoquants. Also, since the upper isoquant indicates a larger input-combination than the lower ones, each successive upper isoquant indicates a higher level of output than the lower ones. 

For example, if isoquant 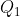 represents an output equal to 100 units, then isoquant 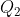represents an output of 200 units which is greater than 100 units.

Marginal Rate of Technical Substitution:

The marginal rate of technical substitution (MRTS) is the rate at which one input can be substituted for another without changing the level of output. The marginal rate of technical substitution (MRTS) is the slope of an isoquant and measures the rate at which the two inputs can be substituted for one another while maintaining a constant level of output.

The minus sign is added in order to make MRTS a positive number since , the slope of the isoquant is negative. The marginal rate of technical substitution also can be expressed as the ratio of two marginal products:

     

As labour is substituted for capital, 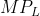 declines and  rises causing MRTS to diminish.

Illustration: To illustrate the MRTS numerically, let us suppose that a given production function may be presented in a tabular form as given below. The table presents 5 alternative combinations of K and L that can be used to produce a given quantity, say 100 units, of a commodity.   

Factor Combinations	Units of Labour (L)	Units of Capital (K)	MRTS
A	1	12
			4
B	2	8
			3
C	3	5
			2
D	4	3
			1
E	5	2

Properties of Isoquants:

1. Isoquants have a Negative Slope: The negative slope of the isoquant implies that if one of the inputs is reduced, the other input has to be so increased that the total output remains unaffected, i.e., the reduction in production due to a reduction in the quantity of input is exactly offset by the output resulting from an increase in the other input. For example, movement from A to B on the isoquant 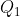 = 100 means that if  of units of capital are removed from the production process,  units of labour have to be employed to maintain the same level of output. 

2. Isoquants are Convex to the Origin: Convexity of isoquants implies not only the substitution of one factor for another but also diminishing marginal rate of technical substitution (MRTS). As mentioned above, the MRTS is the rate at which the marginal unit of an input can be substituted for the other input so that the level of output remains the same. The MRTS decreases because, by assumption, no factor is a perfect substitute for another. For this reason, more and more units of input are needed to replace each successive unit of other input.

3. Isoquants Cannot Intersect or be Tangent to Each Other: If two isoquants one corresponding to 100 units and the other to 200 units of output intersect each other, then there will be a common factor combination corresponding to the point of intersection. It means that the same factor combination which can produce 100 units of output according to one isoquant can also produce 200 units of output according to the other isoquant. But this is quite absurd.  The same factor combination cannot produce two different levels of output, the technique of production remaining unchanged.

4. Higher isoquants represent a higher level of output: Between any two isoquants, the upper one represents a higher level of output than the lower one. The reason is that any point on an upper isoquant implies a larger input combination, which in general, produces a larger output. Therefore, upper isoquants indicate a higher level of output.

Reading Lists:

1) Barthwal, R. R. (1992), Microeconomic Analysis (1st Edition). Wiley Eastern Limited, New Delhi, India.

2) Koutsoyiannis, A. (1990), Modern Microeconomics (2nd edition). Macmillan, London.

3) Henderson, J. M. and R. E. Quandt (1980), Microeconomic Theory: A Mathematical Approach (3rd edition). McGraw Hill, New Delhi. 

4) Samuelson, P. A., & Nordhuas, W.D (1992), Economics (14th edition). McGraw Hill International edition, U.S.

5) Samuelson, P. A., & Nordhuas, W.D (2013), Microeconomics (19th edition). McGraw Hill Education (India) Pvt. Ltd.

6) Dwivedi, D. N. (2016), Microeconomics: Theory and Applications (3rd edition). Vikas Publication House Pvt. Ltd. Noida (UP), India.

Link to the document