Producer’s Equilibrium: The Optimal choice of Inputs

A producer is in equilibrium when he or she maximizes output for the given total outlay. In other words, a producer is in equilibrium when the highest isoquant is reached, given a particular iso-cost or price line. An isoquant (IQ) represents different combinations of labour and capital which yields the same level of output of a commodity. An iso-cost or price line represents the different combinations of labour and capital that an entrepreneur can purchase, given the prices of the two-factor inputs and the total outplay available to the producer at a point of time. Producer’s equilibrium occurs when an isoquant is a tangent to the iso-cost line. At the point of tangency, the absolute slope of the isoquant is equal to the absolute slope of the iso-cost line. That is, at equilibrium, 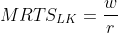  . Since  , at equilibrium,

   

At equilibrium, the MP of the last unit spent on labour is the same as the MP of the unit spent on capital. The same applies to the other factors if the firm’s production function is expressed in terms of more than two factors of production. 

Given the total outlay constraint AB,  is the highest isoquant the firm can reach.  is desirable, but not attainable with the given iso-cost line. Further, at  the firm would not be maximizing output. Therefore, a rational producer who aims at maximum output with the given total outlay, would be at equilibrium at point E, where  .

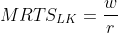
Producer’s equilibrium can be explained either by:

a)Constrained output maximisation (Maximisation of output subject to a cost constraint)

b)Constrained cost minimisation (Minimisation of cost subject to an output constraint)

Constrained Output Maximisation:

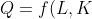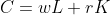
In this approach, we assume output maximisation subject to the budget constraint as the goal of the producer. If the firm’s production function is given by  , and its cost constraint is given by  . The optimization problem is defined as:

     

Using the Lagrange Multiplier Method and combining these two expressions together, the Lagrange function can be defined as:

 

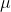
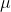
Where,  is the Lagrange multiplier. Taking the partial derivative of Z for L and K and   , the first-order conditions are:

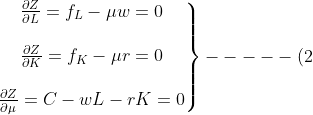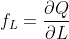
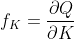
Where,   and,   defined as the marginal product of the input L and K respectively.

From the first two equations of (2), we have,

   

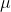
Equating the  , we have

 

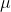
 is a constant defined as the marginal contribution of expenditure  or the marginal product of money. Equation (3) gives us the equilibrium condition for the producer. According to this, the contribution to the output of the last unit of money spent upon each input must be equal and identical to the marginal contribution of money ().  

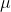
From (3), we get the expression 

We know that

 

Therefore, we have 

 is the slope of the isoquant and     is the slope of the iso-cost line. At equilibrium situation, we have the slope of the isoquant equal to the slope of the iso-cost line. In other words, the iso-cost line is tangent to the isoquant. Representing equation (4) graphically, we have  

Point E is the producer’s equilibrium. At point E, the slopes of both the curves, i.e., isoquant   and the iso-cost line are identical. The iso-cost line is tangent to the isoquant and there is no scope for the producer to move away from this.

The first-order conditions would be valid provided the second-order conditions for output maximisation are satisfied. Such conditions are normally taken in the form of the bordered Hessian determinant of second partial derivatives of Z with respect to L and K and whose value should be positive, i.e., what the second-order conditions have to show is that the rate of change of the slope of the tangent to an isoquant must be positive, i.e.,  at the point of tangency with the iso-cost line. In expanded form, we write the second-order conditions: 

Constrained Output Maximisation:

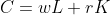
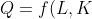In this approach, we assume cost minimisation subject to a given level of output as the goal of the producer. If the firm’s cost is given by    , and its output is given by   . The optimization problem is defined as:

 

Using the Lagrange Multiplier Method and combining these two expressions together, the Lagrange function can be defined as:

   

Where λ is the Lagrange multiplier. 

Taking the partial derivative of Z for L and K and λ, the first-order conditions are:  

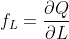
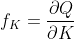
Where,   and,   defined as the marginal product of the input L and K respectively.

From the first two equations of (2), we have, 

Equating , we have 

 

In the expression   , λ is defined as the marginal cost of output i.e., increment in the total cost of production (C) in real terms to produce one more extra unit of output, i.e.,  . It is the inverse of. Therefore, is nothing but   . The producer has to select the cost equation which minimizes the total cost of production of a given level of output Q. This is shown in the figure below: 

Let us consider AB, A’B’ and A”B” as three iso-cost lines showing three possible levels of cost to produce Q output. The combinations of L and K required to produce Q output must lie on the isoquant of Q as well as on the iso-cost line. Therefore, iso-cost line A”B” is not feasible. This rule out the section of the isoquant above R and beyond T and along the line segment RT of the iso-cost line A’B’. At points R and T the slopes of the isoquant and iso-cost lines are different. They are not the equilibrium points. The combinations of L and K shown by R and T points are costly as compared to the combinations shown by the arc RT of the isoquant below the line RT. It is possible to produce Q by shifting down the line A’B’ to eventually AB line. The AB line represents the lowest cost for production of Q. It is tangent to the isoquant Q at point E showing the equilibrium situation and optimum, i.e., least-cost combination of L and K which is L* and K. The second-order conditions for cost minimisation would be the same as that for constrained output maximisation, i.e.,

 

This implies that      , i.e., the rate of change of slope of the isoquant at the point of tangency is positive. The convexity of the isoquant ensures this. 

Reading Lists:

1) Barthwal, R. R. (1992), Microeconomic Analysis (1st Edition). Wiley Eastern Limited, New Delhi, India.

2) Koutsoyiannis, A. (1990), Modern Microeconomics (2nd edition). Macmillan, London.

3) Henderson, J. M. and R. E. Quandt (1980), Microeconomic Theory: A Mathematical Approach (3rd edition). McGraw Hill, New Delhi. 

4) Samuelson, P. A., & Nordhuas, W.D (1992), Economics (14th edition). McGraw Hill International edition, U.S.

5) Samuelson, P. A., & Nordhuas, W.D (2013), Microeconomics (19th edition). McGraw Hill Education (India) Pvt. Ltd.

6) Dwivedi, D. N. (2016), Microeconomics: Theory and Applications (3rd edition). Vikas Publication House Pvt. Ltd. Noida (UP), India.

Link to document