Economics at Zero Marginal Cost: Hawkins-Simon Conditions

In some cases, the Input-Output Model equation [ $\\X=(I-A)^{-1}.F$ ] solution may give output expressed by negative numbers. However, in economic sense, output cannot be negative since a firm may produce some amount of product or no product at all. It cannot produce a negative amount of a product, say, it cannot produce negative 2 units of bread.

If our solution gives negative outputs, it means that more than one unit of a product is used up in the production of every one unit of that product; it is definitely an unrealistic situation. Such a system is not viable.

The solution of Leontief Input-Output model equation, $\\X=(I-A)^{-1}.F$ will yield a non-negative output if and only if its satisfies certain conditions. These conditions are known as Hawkins- Simon conditions. It ensures that the Leontief Input- Output model does not give negative numbers as a solution.

For n-Industries Case:

Given the Leontief matrix [I−A]:

$\begin{bmatrix} \ \1-a_{11}\ \ \ \ \ \ -a_{12}\ ........\ -a_{1n}\\ \ \ \ \ \ -a_{21}\ \ \ \ \1-a_{22}\ ........\ -a_{2n}\\ .................................................\\ .................................................\\ \ \ \ \ \ -a_{n1}\ \ \ \ \ \ \ -a_{n2}\ ........1-a_{nn} \end{bmatrix}$

The two conditions are:

(i) the diagonal elements: $(1-a_{11}), (1-a_{22}),...,(1-a_{nn})$ should all be positive or, in other words, elements, $a_{11},a_{22},...,a_{nn}$ should all be less than one. Thus, the production of one unit of output of any sector should use not more than one unit of its own output, and

(ii) the determinant of the matrix must always be positive.

These two conditions are called Hawkins-Simon conditions.

Economic Interpretation of Hawkins-Simon Conditions

Let us consider 2-industries case. The Leontief matrix [I-A] can be written as:

$\begin{bmatrix} \ \ \1-a_{11}\ \ \ \ \ \ \ \ \ \ -a_{12} \\ \ \ \ \ -a_{21}\ \ \ \ \ \ \ \ \ \1-a_{22} \end{bmatrix}$

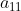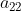1. The first condition requires that $1-a_{11}$ and $1-a_{22}$ must be positive or $a_{11}$ and $a_{22}$ must be less than one. Economically, this implies that the amount of a commodity used in the production of a hundred rupee's worth of that commodity must be less than hundred rupee.

In case of the 1st commodity, the amount of the 1st commodity used in the production of a hundred rupee's worth of the 1st commodity must be less than hundred rupee.
In case of the 2nd commodity, the amount of the 2nd commodity used in the production of a hundred rupee's worth of the 2nd commodity must be less than hundred rupee.

2. The second condition implies that its determinant must be positive i.e. D > 0 implies that $\begin{vmatrix} \ \ \1-a_{11}\ \ \ \ \ \ \ \ \ \ -a_{12} \\ \ \ \ \ -a_{21}\ \ \ \ \ \ \ \ \ \1-a_{22} \end{vmatrix}>0$

$\\or,\ (1-a_{11})(1-a_{22})-a_{12}a_{21}>0\\ or,\ 1-a_{22}-a_{11}+a_{11}a_{22}-a_{12}a_{21}>0$

Transferring all terms involving 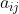$a_{ij}$ to the right-hand side, we have

$\\or,\ 1>a_{22}+a_{11}-a_{11}a_{22}+a_{12}a_{21}\\ or,\ a_{22}+a_{11}-a_{11}a_{22}+a_{12}a_{21}<1\\ or,\ a_{22}-a_{11}a_{22}+a_{11}+a_{12}a_{21}<1\\ or,\ (1-a_{11})a_{22}+a_{11}+a_{12}a_{21}<1$

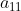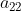Since, $(1-a_{11})a_{22}\$ is positive. According to the first condition, both $a_{11}$ and $a_{22}$ are less than one.

Also, $\\a_{11}+a_{12}a_{21}<1\$

Economically, the first term 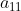$a_{11}$ shows the direct use of the 1st commodity in the production of the 1st commodity itself. The second term shows the indirect use. $\\a_{12}a_{21}\$ shows that output of the 1st industry is used as input in the production of the second commodity which is in turn used as input in the production of the 1st commodity. Economically, the second condition implies that the direct and indirect requirement of any commodity to produce one unit of that commodity must also be less than one.

Economics at Zero Marginal Cost

Pages

Wednesday, June 10, 2020

Hawkins-Simon Conditions

No comments:

Post a Comment

Disturbance term/Error term

Contact Form