Singular and Non-singular Matrix

A singular matrix is a square matrix whose corresponding determinant is equal to zero. 

If A is a square matrix then Matrix A is singular if |A|=0. 

A non-singular matrix is a square matrix whose corresponding determinant is not equal to zero.

If A is a square matrix then Matrix A is non-singular if |A|≠0. 

Exercise 1

Test whether the following matrix is singular:

Solution:

Given: 

To find: Determinant of A, |A|

Since the determinant of matrix A is zero, .i.e., |A|=0.

Hence, the given matrix A is a singular matrix.

Exercise 2

Show that the given matrix is non-singular:

Solution:

Given:

To find: Determinant of B, |B|

Since the determinant of matrix B is not equal to zero, .i.e., |B|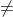0.

Hence, the given matrix B is a non-singular matrix.