Economics at Zero Marginal Cost: The concept of Derivative and Its Application in Economics

Consider an independent variable 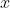$x$ and a dependent variable 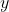$y$ , so that 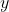$y$ is a function of 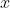$x$ . We choose to write this relationship as:

$y=f(x)$

When variable 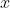$x$ changes from the value 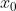$x_{0}$ to a new value 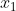$x_{1}$ , the change is measured by the difference $x_{1}-x_{0}$ .

Using the symbol ∆ to denote change, we write

$\Delta x=x_{1}-x_{0}$

The derivative of y with respect to 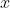$x$ at the point 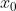$x_{0}$ is defined to be the limit of the ratio of the change in 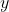$y$ to the change in 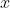$x$ , i.e.,

$\lim_{\Delta x\rightarrow 0}\frac{\Delta y} {\Delta x}\ \ \ or\ \ \lim_{\Delta x\rightarrow 0}\frac{f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}\\$

where $\frac{\Delta y}{\Delta x}=\frac{f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}$ is the difference quotient which measures the average rate of change of $y$ .

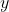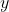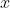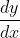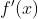The two most common ways of writing notation for the derivative of $y$ with respect to $x$ are either as $\frac{dy}{dx}$ or as $f'(x)$ or simply $f'$ .

$\frac{dy}{dx}=f'(x)=\lim_{\Delta x\rightarrow 0}\frac{\Delta y} {\Delta x}\\$

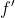The Economics of a Derivative (Application of Derivative in Economics):

In economics a derivative typically represents a marginal concept.

If benefits (B) and costs (C) depend on the level of an activity (x), then the derivative of B with respect to x represents marginal benefit and the derivative of C with respect to x represents marginal cost.

If revenue depends on the quantity of a good sold, then the derivative of revenue with respect to quantity represents marginal revenue.

If production depends on labour input, then the derivative of production with respect to labour input represents the marginal product of labour.

In economics, the marginal cost is usually defined as $MC=\frac{\Delta C} {\Delta x}\\$ and represents the cost of producing one more (or the last) unit. Therefore, Marginal Cost is the derivative of the cost function: $MC=\frac{dC} {d x}\\$ or $MC=C\ '(x)$ . An advantage of using the $C\ '(x)$ notation is that it emphasizes that marginal cost is itself a function of $x$ .

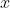Other Marginal Concepts in Economics:

Marginal Utility, $MU=\frac{dTU}{dx}$